Φυσική κατεύθυνσης Γ Λυκείου - Απλή Αρμονική Ταλάντωση - Διάσπαση

Προβλήματα στις Ταλαντώσεις

4ο Πρόβλημα

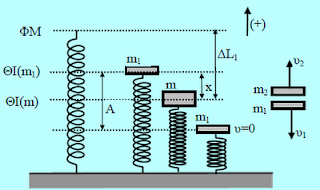
Σώμα μάζας m είναι στερεωμένο στο άνω άκρο ιδανικού ελατηρίου, σταθεράς k = 200N/m το κάτω άκρο του οποίου είναι ακλόνητα στερεωμένο σε οριζόντιο δάπεδο. Το σύστημα αρχικά ισορροπεί με το ελατήριο να είναι συσπειρωμένο κατά ΔL₁= 10cm. Τη στιγμή t = 0 με εσωτερική έκρηξη, το σώμα διασπάται σε δύο τμήματα με μάζες m₁ και m₂ με σχέση μεταξύ τους m₂= 3m₁. 

Μετά τη διάσπαση, που θεωρούμε ότι έγινε πρακτικά ακαριαία, το τμήμα μάζας m₁ παραμένει στερεωμένο στο άνω άκρο του ελατηρίου, ενώ το άλλο τμήμα μάζας m₂ κινείται κατακόρυφα προς τα επάνω και φτάνει σε ύψος h = 1,8m από την αρχική θέση ισορροπίας του σώματος μάζας m πριν την έκρηξη. Να βρεθούν:

α) Το πλάτος και η κυκλική συχνότητα της α.α.τ που θα εκτελέσει το σώμα μάζας m₁ μετά τη διάσπαση.

β) Η ενέργεια που εκλύθηκε κατά τη διάσπαση αν γνωρίζουμε ότι το 25% αυτής μετατράπηκε σε θερμική και το υπόλοιπο σε κινητική ενέργεια των θραυσμάτων.

γ) Το έργο της δύναμης του ελατηρίου κατά το χρονικό διάστημα από τη στιγμή t = 0 μέχρι τη στιγμή που το σώμα μάζας m₁ μηδενίζει για 1^η φορά την ταχύτητά του.

Δίνεται g = 10m/s² και θετική φορά θεωρείται η προς τα επάνω.

Η απάντηση από ΕΔΩ