Φυσική προσανατολισμού Γ Λυκείου - Ισορροπία - στροφική κίνηση Στερεού

Ισορροπία και στροφική κίνηση ράβδου 

(άσκηση 11)

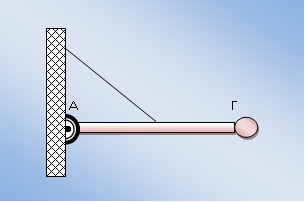
Μια ομογενής ράβδος ΑΓ, που έχει μήκος L=1m και μάζα M=6kg, έχει στο άκρο της Γ μόνιμα στερεωμένο ένα σώμα μικρών δμε μάζα m=2kg.ιαστάσεωνΗ ράβδος στηρίζεται με το άκρο της Α μέσω άρθρωσης και αρχικά διατηρείται οριζόντια με τη βοήθεια νήματος, το ένα άκρο του οποίου είναι δεμένο στο μέσο της ράβδου και το άλλο σε κατακόρυφο τοίχο, όπως στο σχήμα. Η διεύθυνση του νήματος σχηματίζει γωνία φ = π/6 rad με τη διεύθυνση της ράβδου στην οριζόντια θέση ισορροπίας.   

Α. Να υπολογίσετε:

α) το μέτρο της τάσης του νήματος

β) τη ροπή αδράνειας του συστήματος ράβδου - σώματος ως προς άξονα που διέρχεται από το Α και είναι κάθετος στο επίπεδο του σχήματος.

Β. Κάποια στιγμή το νήμα κόβεται και η ράβδος μαζί με το σώμα που είναι στερεωμένο στο άκρο της, αρχίζει να περιστρέφεται στο επίπεδο του σχήματος. Θεωρώντας τις τριβές αμελητέες να υπολογίσετε το μέτρο:

α) της γωνιακής επιτάχυνσης του συστήματος ράβδου-σώματος ως προς τον άξονα περιστροφής μόλις κόβεται το νήμα.

β) την ταχύτητα του σώματος στο άκρο της ράβδου, όταν αυτή φτάνει στην κατακόρυφη θέση.

Δίνονται για τη ράβδο η ροπή αδράνειας της ως προς άξονα που διέρχεται από το κέντρο μάζας της και είναι παράλληλος στον άξονα περιστροφής Ιcm = MR²/ 12.

(εξετάσεις Εσπερινών Λυκείων 2005)

               

Σε pdf από ΕΔΩ